[最も人気のある!] 1 1/2 1/4 ... 1/n sum formula 997348-What is sum of 1/n
You can put this solution on YOUR website!The partial sums of the series 1 2 3 4 5 6 ⋯ are 1, 3, 6, 10, 15, etcThe nth partial sum is given by a simple formula = = () This equation was knownHarmonic Series is Divergent It is understood that the series is unlimited The question is whether the convergent or divergent is the sequence ?

Harmonic Series And 𝑝 Series Video Khan Academy
What is sum of 1/n
What is sum of 1/n-May 27, · In this problem, we are given a number n that defines the nth term of the series Our task is to create a program to find sum of series 1*2*3 2*3*4 3*4*5 n*(n1)*(n2) in C Problem description − Here, we will find the sum till n term of the given series with is 1*2*3 2*3*4 3*4*5 n*(n1)*(n2) This can be decoded as the summation of n*(n1)*(n2)Is there any formula for this series "1 1/2 1/3 1/n = ?" I think it is a harmonic number in a form of sum(1/k) for k = 1 to n
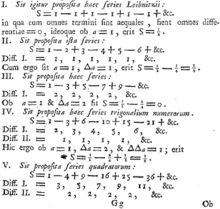


1 2 3 4 Wikipedia
N * (1 1/2 1/3 1/4 1/n) Unlike the geometric series the harmonic series does not converge, but it diverges as we add more terms The partial sums of first n terms can be bounded above and below by ln n C , hence the time complexity of the entire algorithm is θ(n log n)Sep 28, 19 · Determine a formula for the sum 1 1/2 1/3 1/4 1/n?This is one of those questions that have dozens of proofs because of their utility and instructional use I present my two favorite proofs one because of its simplicity, and one because I came up with it on my own (that is, before seeing others do it it's known)
Question Find A (short) Formula For The Sum 1/1 2 1/2 3 1/n(n 1) = Sigma^n_k = 1 1/k(k 1);The partial sums form a convergent sequence 1, 2/3, 1, 4/5, 1, 6/7, The sequence converges to 1 Grouping pairs of successive terms leads to every other sum being omitted but does not change the fact of convergence, nor affects the limit itself The second series to consider is 1/1 2/3 2/3 3/5 3/5 4/7The general formula for the partial sums is, () 2 2 1 3 1 1 1 4 2 2 1 n n i s i n n = = = − − − ∑ and in this case we have, () 3 1 1 3 lim lim 4 2 2 1 4 n n n s n n →∞ →∞ = − − = The sequence of partial sums converges and so the series converges also and its value is, 2 2 1 3 1 4
Two sample induction problems 1 Find a formula for 1 4 7 (3n 2) for positive integers n, and then verify your formula by mathematical inductionCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyFor the proof, we will count the number of dots in T(n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division!



How To Sum The Integers From 1 To N 8 Steps With Pictures


What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora
A Simple Solution solution is to initialize sum as 0, then run a loop and call factorial function inside the loop Following is the implementation of simple solution1 2 1 4 1 8 with a sum going on forever Once again we can use sigma notation to express this series We write down the sigma sign and the rule for the kth term But now we put the symbol for infinity above the sigma, to show that we are adding up an infinite number of terms In this case we would have X∞ k=1 1 2k = 1 2 4 1 8Visit https//wwwmathmunicom/ for thousands of IIT JEE and Class XII videos, and additional problems for practice All free Over 1 million lessons deliver



Ex 9 4 1 Find Sum Of Series 1 X 2 2 X 3 3 X 4 Ex 9 4



Formula 1 2 3 4
Excel in math and science Log in with Facebook Log in with Google Log in with email Join using Facebook Join using Google Join using emailJan 05, 17 · sum_(i=1)^n (1i/n)(2/n) = (3n1)/n lim_(n rarr oo)sum_(i=1)^n (1i/n)(2/n) = 3 > Let S_n = sum_(i=1)^n (1i/n)(2/n) S_n = sum_(i=1)^n (2/n(2i)/n^2) S_n = 2/nPartial sum of an infinite series If n driven to



Harmonic Series And 𝑝 Series Video Khan Academy
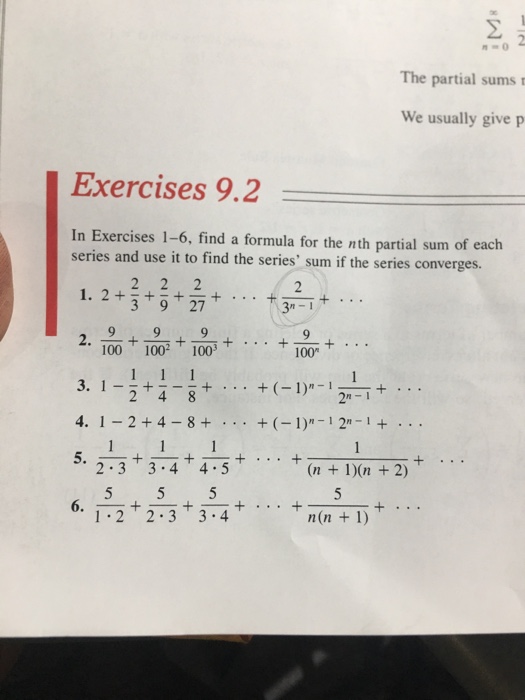


Solved In Exercises 1 6 Find A Formula For The Nth Parti Chegg Com
By signing up, you'll get thousands of stepbystepClick here 👆 to get an answer to your question ️ Write a program to find the sum of the following series s= 1/2 1/4 1/8 1/16 to n terms hhhhyyrfft hhhhyyrfftSep 14, 10 · Now sum up (*) for texk = 1, 2, \dots , n/tex The sum on the left hand side telescopes, leaving tex(n1)^3 1/tex The sum on the right hand side is tex3 \sum_{k=1}^n k^2 3 \sum_{k=1}^n k n/tex Now equate these two expressions for the sum, apply the formula you already know for tex\sum_{k=1}^n k/tex and solve for tex\sum
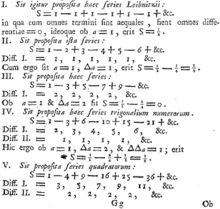


1 2 3 4 Wikipedia



Find Sum Of The Following Ap 1 1 N 1 2 N 1 3 N Upto Nth Terms Brainly In
Find the common difference by subtracting any term in the sequence from the term that comes after it a_2a_1=31=2 a_3a_2=53=2 a_4a_3=75=2 a_5a_4=97=2You can put this solution on YOUR website!Each of these series can be calculated through a closedform formula The case a = 1, n = 100 a=1,n=100 a = 1, n = 1 0 0 is famously said to have been solved by Gauss as a young schoolboy (k^2(k1)^2\big) = 2 \sum_{k=1}^n k \sum_{k=1}^n 1 k = 1 (n 1) 2 n s 3, n = 1 4 n 4 1 2 n 3 3 4 n 2 1 4 n



Example 1 Find Partial Sums Solution S 1 1 2 0 5 S 2 S 3 Find And Graph The Partial Sums S N For N 1 Ppt Download
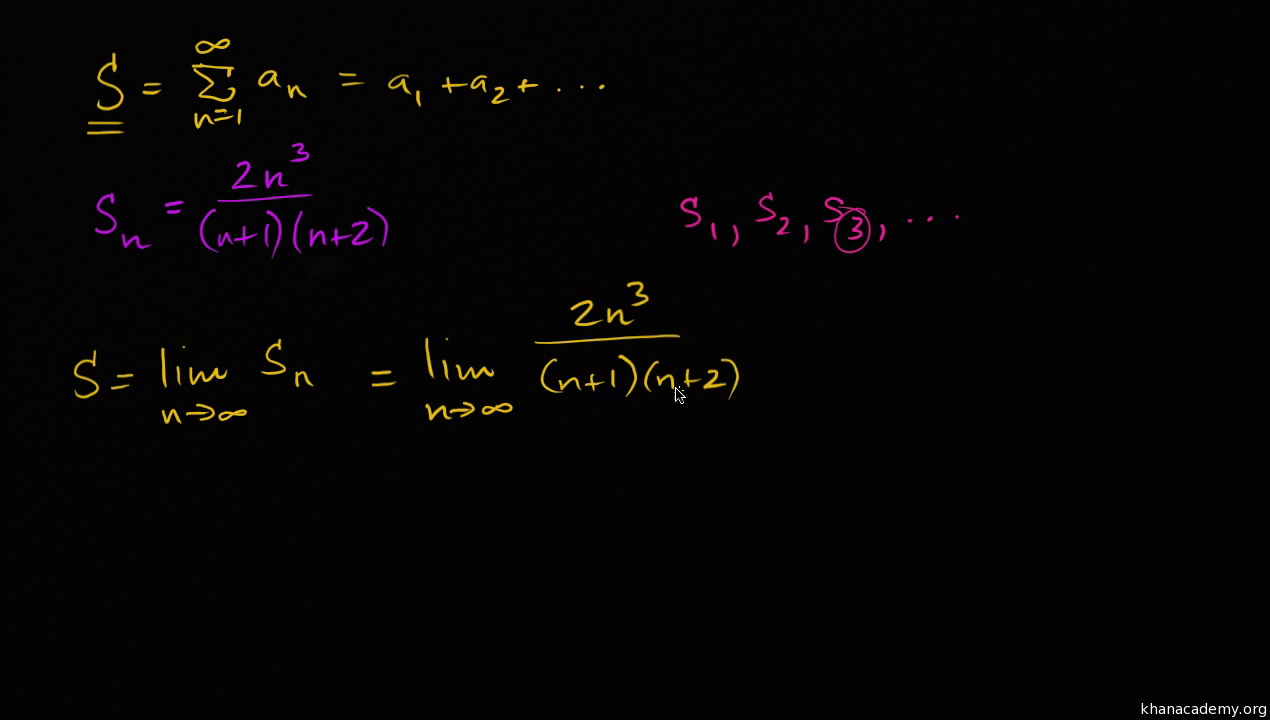


Infinite Series As Limit Of Partial Sums Video Khan Academy
To do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T(4)=1234 =I have tried finding many different patterns within this sum to determine a general formula however I have been stuck on this Any help would be appreciatedWhat is the sum of 1*2 2*3 (n1)n?



Find The Sum Of N Terms Of The Series 1 2 4 1 4 6



Find 4 1 N 7 2 N 10 3 N Upto N Terms Class 10 Brainly In
To prove that To prove it using induction 1) Confirm it is true for n = 1 It is true since 1/2 = 1/2^1 2) Assume it is true for some value of n = k ie > eqn (1) 3) Now prove it is true for n = k1 ie the sum up to (k1) terms = 1 1/2^(k1) Proof For n = k1, the expression of the sum is = > from eqn(1) = > taking common denominatorWe prove the formula 1 2 n = n(n1) / 2, for n a natural number There is a simple applet showing the essence of the inductive proof of this result To run this applet, you first enter the number n you wish to have illustrated;Space limitations require 0



Geometric Series Wikipedia



Ex 9 4 4 Find Sum Of Series 1 1 X 2 1 2 X 3 1 3 X 4
S_n = 123n with n1 additions can be expressed compactly by Gauss formula as n*(n1)/2 where the number of operations is three and (so it does not depend on n) INov 06, 11 · Find the sum 1 1/2 1/4 1/8 1/16 The answer is 2/3, but I don't get how to get to this There's a formula for finding the sum, but I cant find it in my discrete math bookThen Prove, Using Induction, That Your Formula Is Correct 1/1 2 = 1/2, 1/1 2 1/2 3 = 1/2 1/6 = 2/3, 1/1 2 1/2 3 1/3 4 = 2/3 1/12 = 8/12 1/12 = 3/4, And 1/1 2 1/2 3 1/3 4 1/4 5 = 3/4 1/ = 15/ 1/ = 4/5 This Leads Us To Suspect That



Solved Using Formula 2 Find The Sum Of The Series Sigma Chegg Com



Find The Sum Of The Series Sum N 1 Infty Frac 3n 2 N Mathematics Stack Exchange
Feb 06, 10 · this is what is known as a power series your first series 1/1 1/2 1/3 1/n = Sum{1/n}n=1>inf if you are familiar with the notation, the Sum is the big sigma, the n=1 goes underneath and is know as the index, and the inf goes ontop and is know as the limitAnswer to Sum n=1 ^4 1/n=1/11/21/31/4=25/12 How do you solve this without a calculator?Let, {Sn} = u1 u 2 u 3 u 4 u n;



Paradox 1 1 2 1 3 1 4 0 The Simpsons And Their Mathematical Secrets


Key Concepts In Computer Science Assignment 10 All Test Answers
What a big sum!So we can construct f(n) = f(n1) 1/(n(n1)) Now look at the small values of n f(1) = 1/2, f(2) = 1/2 1/6 = 2/3, f(3) = 2/3 1/12 = 3/4, f(4) = 3/4 1/ = 4/5, etc So for the first few small values of n, we have proven by demonstration that f(n) = n / (n1)Sum from a to n = n * (n 1) / 2 – (a 1) * a / 2 We want to get rid of every number from 1 up to a – 1 How about even numbers, like 2 4 6 8 n?



Misc 23 Find Sum Of Series 3 7 13 21 31 Miscellaneous



Infinite Series
Find the sum to n terms of the series 1/(11^21^4) 2/(12^22^4) 3/(13^23^4) The general term is t n = n/(1n 2 n 4 ) = ½ 1/(n 2 n1) – 1/May 07, · Given a positive integer N, the task is to find the sum of the series 1 – (1/2) (1/3) – (1/4) (1/N) using recursion Approach The idea is to form a recursive case and base case in order to solve this problem using recursion Therefore Base Case TheMay 27, · In this problem, we are given a number n Our task is to create a program to find sum of series 1 1/2 1/3 1/4 1/n in C Code description − Here, we will find the sum of the series 1 1/2 1/3 1/4 1/n till nth term The series is a harmonic progression series Harmonic progression is a series whose inverse will be an arithmetic progression



Find The Sum Of N Terms Of The Series 1 2 4 1 4 6



Is There Any Elementary Formula For The Sequence Sum K 1 N Left 2k 1 Right Left Frac 1 2 Right K Mathematics Stack Exchange
Dec 29, · Example \(\PageIndex{1}\) Showing series diverge Let \(\{a_n\} = \{n^2\}\) Show \( \sum\limits_{n=1}^\infty a_n\) diverges Let \(\{b_n\} = \{(1)^{n1}\}\)Contribute your code and comments through Disqus Previous Write a C program that accepts 4 real numbers from the keyboard and print out the difference of the maximum and minimum values of these four numbers Next Write a C program to create enumerated data type for 7 days and display their values in integer constantsWeekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelled



Math 1210 Solutions To Assignment 1 Fall 12 1 A Use



What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora
Apr 12, 21 · Given a positive integer n, write a function to compute sum of the series 1/1!Enter the world of Formula 1 Your goto source for the latest F1 news, video highlights, GP results, live timing, indepth analysis and expert commentaryWrite out a bunch of the sums 1*2 = 2 1*2 2*3 = 2 6 = 8 1*2 2*3 3*4 = 8 12 = 1*2 2*3 3*4 4*5 = = 40 1*2 2*3 3*4 4*5 5*6 = 40 30 = 70 1*2 2*3 3*4 4*5 5*6 6*7 = 70 42 = 112 Make a difference table List those partial sum in a column



If S 1 S 2 S 3 S N Are The Sums Of Infinit



In Showing Integer Sum 1 2 3 N By L Hopital Rule Why They Take Lim As R Approaches To 1 In One Of Steps Why 1 Mathematics Stack Exchange
One can write $$1\frac12\frac13\cdots\frac1n=\gamma\psi(n1)$$ where $\gamma$ is Euler's constant and $\psi$ is the digamma function Of course, one reason for creating the digamma function is to make formulae like this trueJul 04, 17 · I won't go into a full explanation as it too complex But essentially Sum of the reciprocals sum_(r=1)^n \ 1/r = H_n Where H_n is the nth harmonic number Sum of the reciprocals of the squares sum_(r=1)^n \ 1/r^2 = pi^2/6 sum_(r=1)^n \ (beta(k,n1



Find The Sum Of The Series 1 1 2 1 2 3 1 2 3 4



Solved Write The Sum In Sigma Notation 1 2 2 3 3 4 Chegg Com



Intro To Series What Is 1 2 1 4 1 8 1 16 Youtube


What Is The Formula For Finding The Sum Of The Integers 1 4 10 35 And 56 That Appear In A Diagonal Row In Pascal S Triangle Quora



Example 25 Find Integral X2 1 Dx As Limit Of A Sum Examples



Show That The Sum Of The Cubes Of The First N Natural Numbers Equal



Evaluate The Limit Of Sum Limits I 1 N Frac 2 N Left Left Frac 3i N Right 3 Frac 5i N 2 Right When N To Infty Mathematics Stack Exchange



Solved Find A Formula For The General Term A N Not The P Chegg Com



Program To Find Sum Of First N Natural Numbers Geeksforgeeks



Partial Sums Formula For Nth Term From Partial Sum Video Khan Academy



Sums Sumatorias
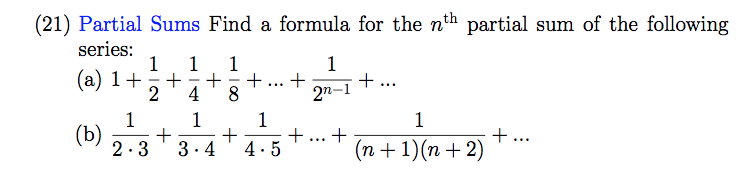


Solved Partial Sums Find A Formula For The N Th Partial S Chegg Com


What Is The Name For The Pattern 1 2 4 8 16 What Is The Formula To Determine A Known Position In The Pattern Quora


What Is S Sum To Terms For Arithmetic Sequence 1 4 7 10 Quora
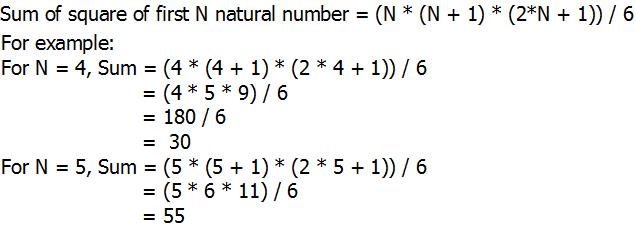


Python Program For Sum Of Squares Of First N Natural Numbers Geeksforgeeks



How To Prove A Formula For The Sum Of Powers Of 2 By Induction Mathematics Stack Exchange



Example 19 Find Sum Of Series 5 11 19 29 41


n Sum Formula


What Is The Sum Of 1 1 3 2 1 3 3 1 3 N Quora


What Is The Sum Of 1 4 9 16 Up To The 50th Terms Quora



How To Solve Fraction Questions In Math 10 Steps With Pictures



How To Sum The Integers From 1 To N 8 Steps With Pictures


C Program To Find The Sum Of Series 1 4 2 4 3 4 N 4 Stack Overflow


1234n Formula



Ali Added The Following Series If Fraction How Many More Fraction In This Series He Must Add To Get The Answer Equal To Onevor More Than One 1 2 1 4 1 Mathematics Topperlearning Com 8ycaaeuu
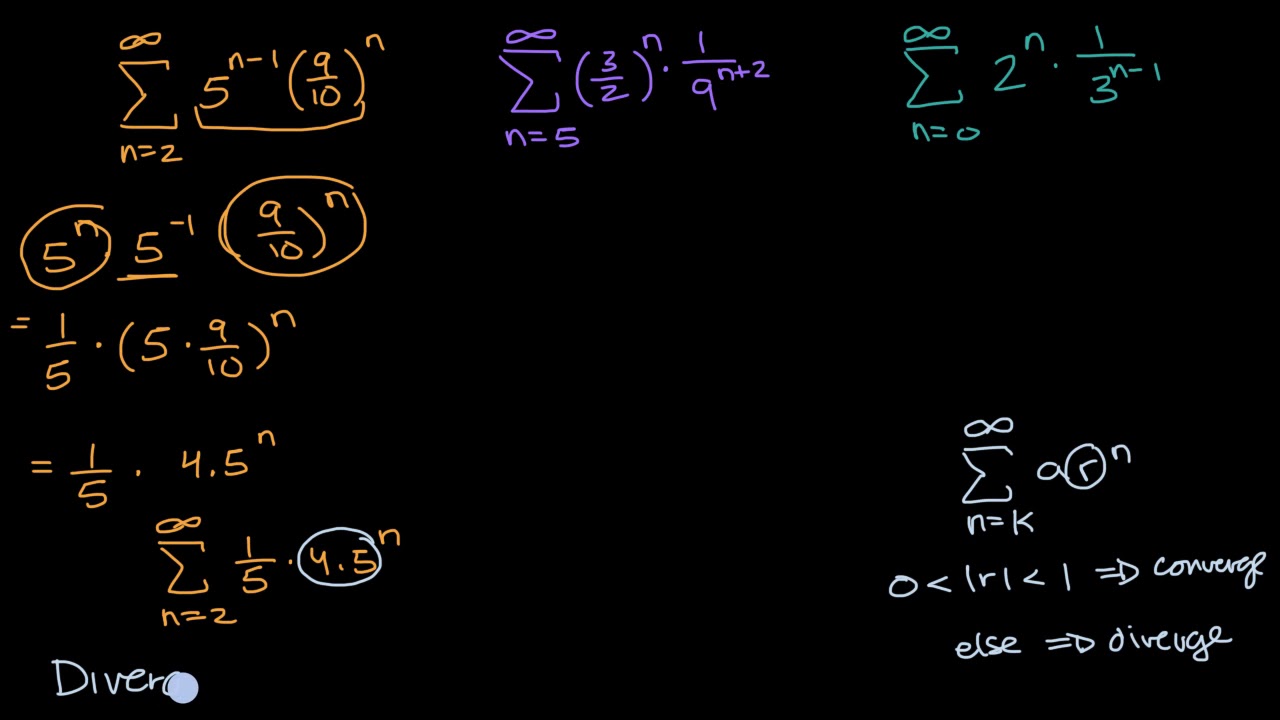


Convergent Divergent Geometric Series With Manipulation Video Khan Academy



Solved Consider The Conditionally Convergent Series Sigma Chegg Com



1 2 1 4 1 8 1 16 Wikipedia



1234n Formula



Find The Sum Of 4 1 N 4 2 N 4 3 N Up To The Nth Term Brainly In



Example 1 Find Partial Sums Solution S 1 1 2 0 5 S 2 S 3 Find And Graph The Partial Sums S N For N 1 Ppt Download



1 2 1 4 1 8 1 16 Wikipedia


What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora



What Will Be Series Of 2n Sum Formula Quora



Stolz Cesaro Theorem Online Presentation
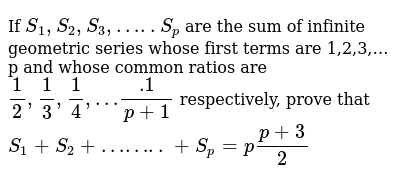


If S 1 S 2 S 3 S P Are The Sum Of Infinite Geometric Serie


Q1 Sum Of The Series 1 123 5 345 9 567 Till Infinity Q2 Find Value Of Log 1 1 N N Mathematics Topperlearning Com Qyqyjc



Sums Sumatorias



Example 1 Find Partial Sums Solution S 1 1 2 0 5 S 2 S 3 Find And Graph The Partial Sums S N For N 1 Ppt Download



Geometric Series Wikipedia



How Do I Find The Sum Terms Of Geometric Sequences And Series Ppt Download
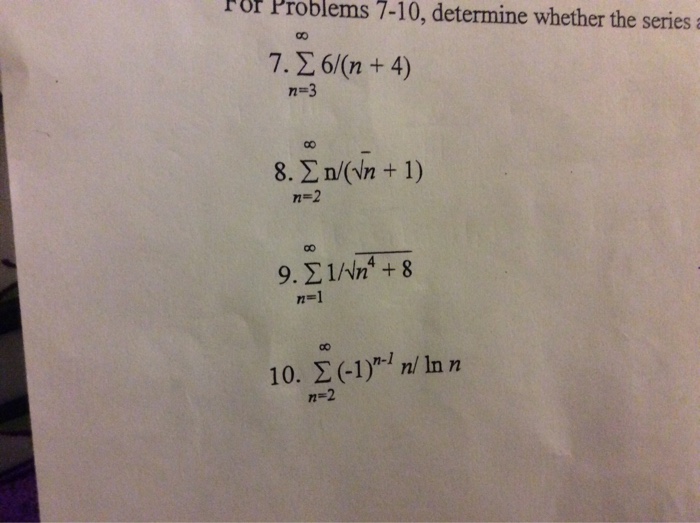


Solved 1 Determine Whether The Series Converge Or Diverg Chegg Com


What The Sum Of 1 1 2 1 3 2 1 5 2 1 2n 1 2 Quora



An Introduction To Mathematical Induction The Sum Of The First N Natural Numbers Squares And Cubes Math Wiki



Understand The Formula For Infinite Geometric Series Video Lesson Transcript Study Com



How To Find 1 2 1 4 1 8 Math Class 21 Video Study Com



Proof By Induction Wolfram Demonstrations Project



n Sum Formula


How Does 1 2 1 4 1 8 1 16 Till Infinity Have A Sum Quora


Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot


What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora



Ex 9 4 2 Find Sum 1 X 2 X 3 2 X 3 X 4 3 X 4 X 5
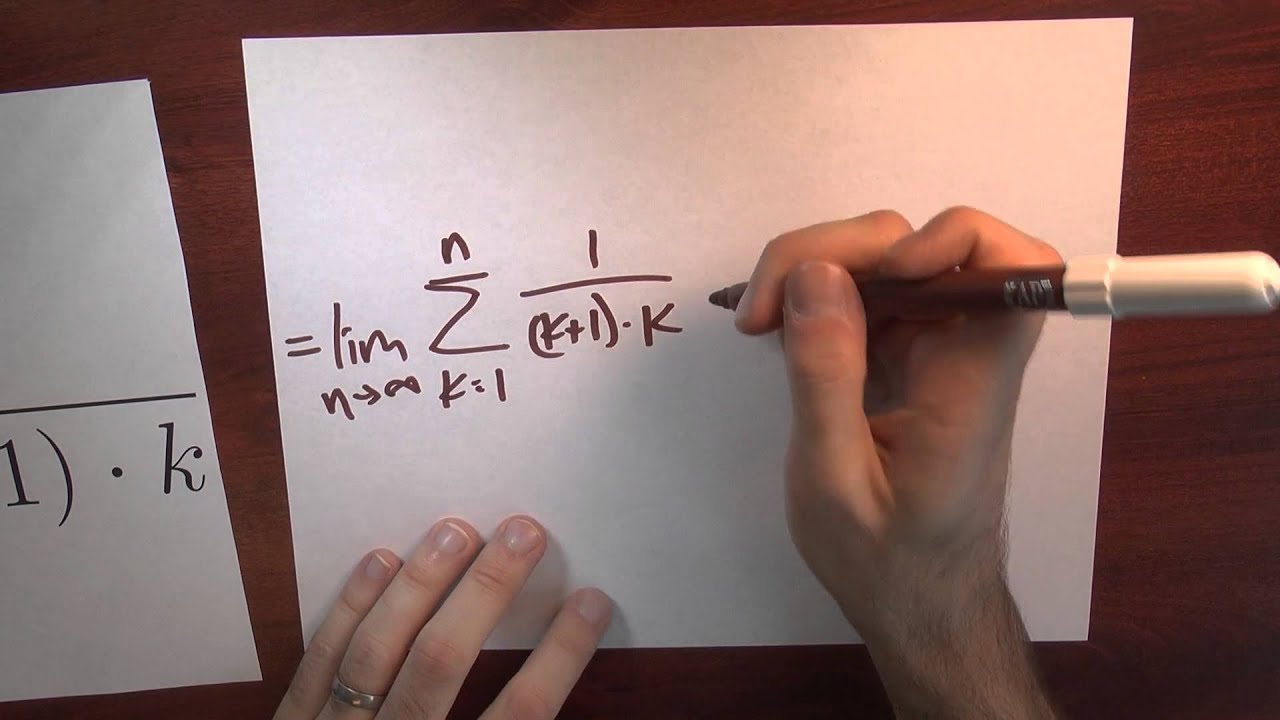


What Is Sum 1 K 1 K Week 2 Lecture 5 Sequences And Series Youtube


Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot



Find The Sum Of N Terms Of The Series 1 2 4 1 4 6



Proof By Induction Wolfram Demonstrations Project



Solved A Using Formula 2 Find The Sum Of The Series Si Chegg Com



Basel Problem Wikipedia



Understanding The Proof That The Series Sum Frac 1 N 2 Is Convergent Mathematics Stack Exchange



Solved Find A Formula For The General Term An Not The Pa Chegg Com



What Is The Summation Of 2 4 8 16 1024 Mathematics Stack Exchange



1 2 3 4 Wikipedia



How To Proceed Further In This Arithmetico Geometric Progression Problem Mathematics Stack Exchange



Derivation Formula Sum Of First N Squares Or Square Numbers 1 2 2 2 3 2 4 2 N 2 Youtube


n2 Formula



Divergence Of The Sum Of The Reciprocals Of The Primes Wikipedia



Proof 1 1 1 4 1 9 1 16 1 25 Pi 2 6 Youtube
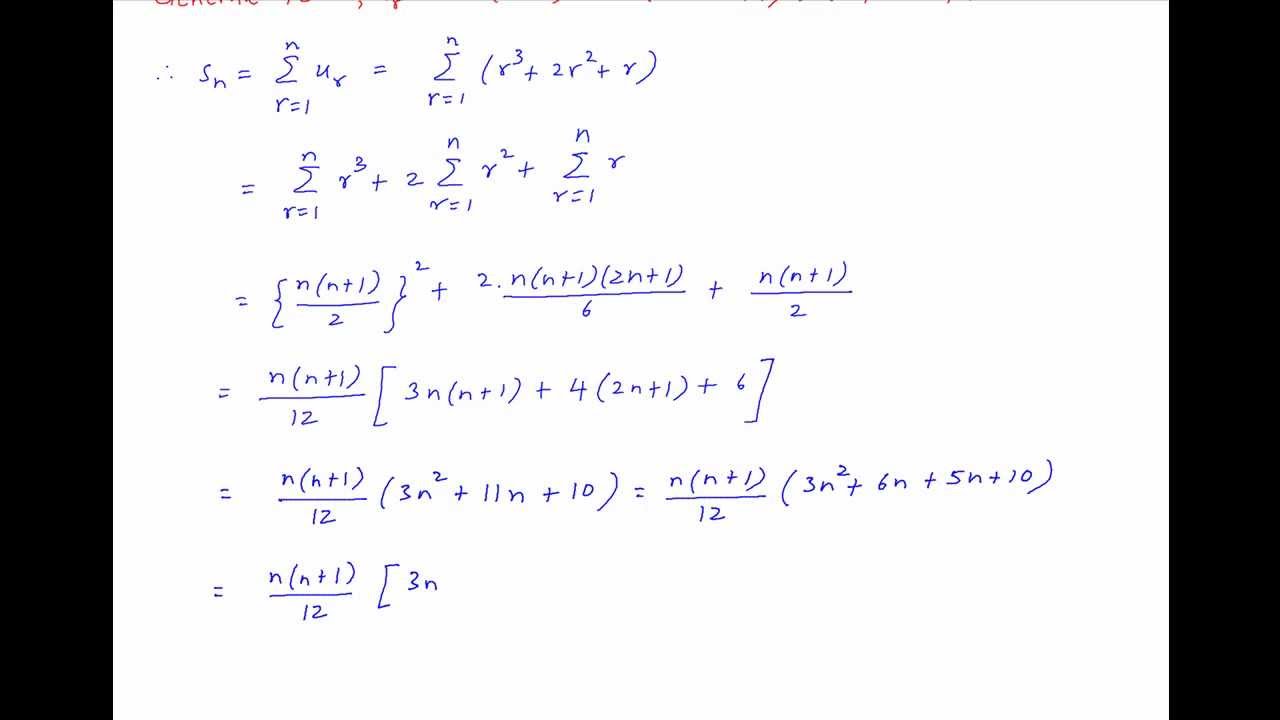


Sum To N Terms 1 2 2 2 3 2 3 4 2 Youtube



Find The Sum Of The Series 1 2 4 Upto 9 Terms Using The Formula



Prove By Induction Sum Of The First N Cubes 1 3 2 3 3 3 N 3 Youtube
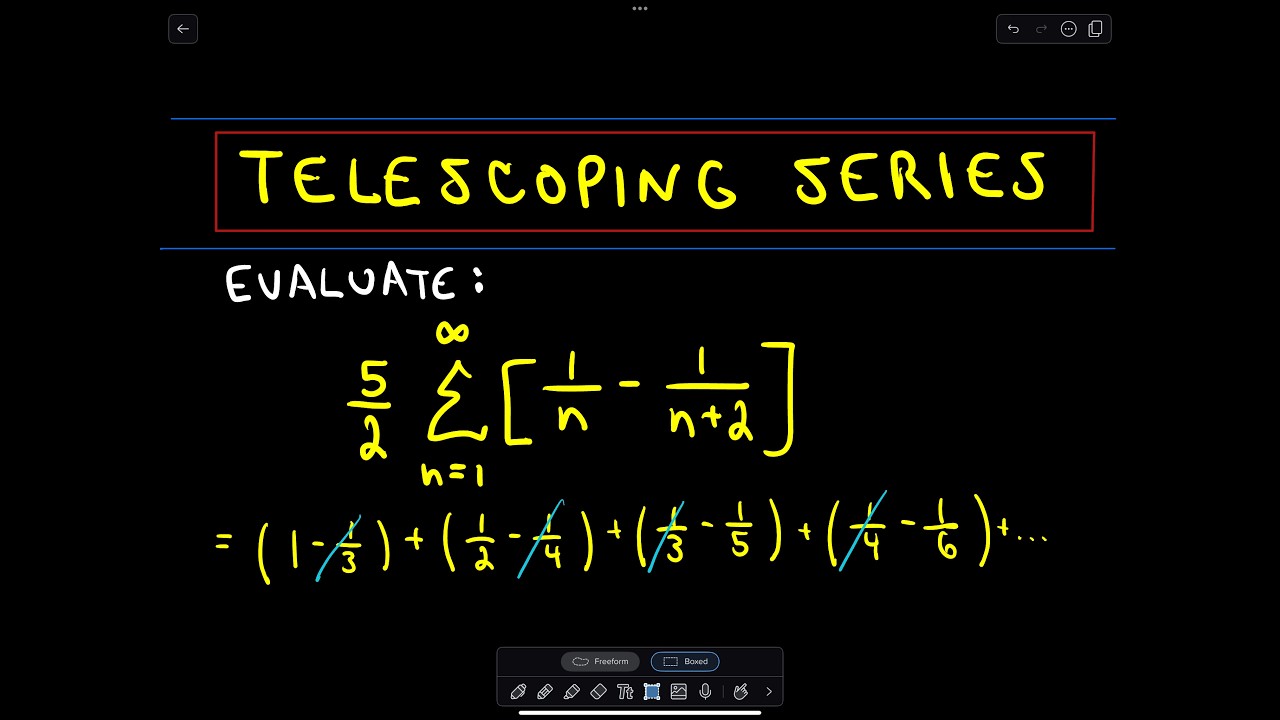


Telescoping Series Finding The Sum Example 1 Youtube



Basel Problem Wikipedia



n Sum Formula



Rd Sharma Solutions For Class 11 Chapter 19 Arithmetic Progressions Download Free Pdf


コメント
コメントを投稿